- Introduction[1]
In this paper, I aim to reconstruct the role that the reference to cognition plays in transcendentalist and non-transcendentalist accounts on the nature of geometry and space. Indeed, if the nature of the mind is directly brought into play by Kant, it is harder to imagine such a thing happening for non-transcendentalist views. However, I want to show that some scientists, while eradicating Kant’s claim, deploy examples that hinge on the constitution of subjects’ minds.
To prove this, I will divide the paper into three parts. In the second section, I will briefly address Kant’s arguments on the subjectivity of space and spatial cognition. In the third section, I will deal with von Helmholtz’s attack in order to highlight its twofold character. In the fourth section, I will survey Poincaré’s position. Besides, the discussion on Kant argument will compel us to scrutinise both the analytic-synthetic distinction and the question about the empiricist or conventional character of axioms. The final section will contain concluding remarks.
- Kant
In this section, I will approach Kant’s reflection on the importance of human cognition when dealing with the representation of space. I will begin with Allgemeine Naturgeschichte und Theorie des Himmels, which is usually overlooked in the debate upon the philosophy of geometry. Kant’s Allgemeine Naturgeschichte is in fact famous for having influenced posterior cosmology and its theological references[2], rather than for its geometrical concerns. Nevertheless, one of the most ‘creative’ assumptions made by the philosopher in the third section of this work may be of interest for our purpose. In essence, after assuming that it is highly improbable that in our galaxy there would not be other living beings, Kant claims that their sensibility is affected by the external world in different degrees depending on the distance from the sun of the planets in which they live, as these two excerpts display:
Most of the planets are certainly inhabited and those that are not will be at some stage. Now what sort of circumstances will be caused among the various kinds of these inhabitants by the relationship of their place in the solar system to the center point from which the heat that gives life to everything emanates? […] The human being, who is the one among all rational beings we are most familiar with […] will have to serve as the basis and general reference point in this comparison. We shall consider him here not from the point of view of his moral qualities, nor from the physical aspects of his build, we shall examine only the limitations that his ability to think rationally and the motion of his body that obeys this ability would suffer as a result of the constitution of the matter to which he is bound and which is proportionate to the distance from the Sun. […] It is […] certain that the human being, who derives all his concepts and ideas from the impressions the universe stimulates in his soul through his body, depends totally on the constitution of this matter to which the creator has bound him for both their clarity as well as the skill to connect and compare them, which we call the faculty to think[3].
The excellence of thinking nature, the sprightliness of their ideas, the clarity and liveliness of the concepts they receive through external impressions, along with the faculty to put them together, and finally also the agility in the actual exercise, in short, the entire extent of their perfection stands under a certain rule, according to which they become more and more excellent and perfect in proportion to the distance of their domiciles from the Sun[4].
The narrative of such passages sets so to speak a benchmark in Kant’s system, which reminds us that the nature of subjects will be interwoven with the physical conditions that determine the constitution of space and the universe.
Nevertheless, I am well aware that the turn towards critical philosophy did not leave Kant’s argument unaltered. In particular, two matters are relevant. First, Kant felt the exigency during the 1770s of relocating the concept of synthesis in the mind. It thus turned out that space is
nothing external, rather it is the condition of the form of all outer representations subsisting in the mind itself. It is nothing imagined (ens imaginarium). For it is the sole real condition of the representation of real outer things. The order of things that are next to one another is not space, rather space is that which make such an order or better coordination in accordance with determinate conditions possible[5].
By borrowing Torretti’s definition, if one understands intuition as “visualisation”, one then knows it is a «kind of imaginative representation of spatial figures which we all have had while attempting to solve a problem in elementary geometry with closed eyes»[6]. If I were to give a graphical representation, I would opt for the following:
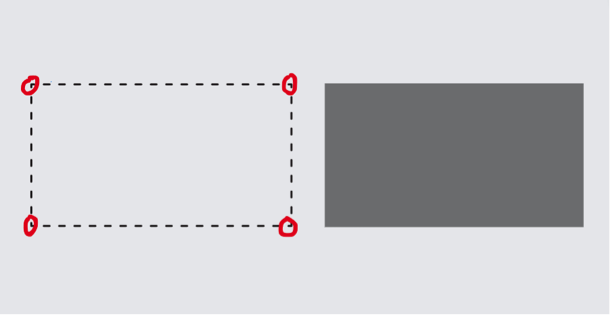
Figure 1––On the left, space is constructed empirically starting from the distances between points (for the sake of clarity, I assumed vertexes of a rectangle to build up distances). This position has been defended by Leibniz among others. On the right, Kant’s intuition: ‘space’ is visualised immediately, which bears witness to the existence of a mental cognition that synthesises empirical data.
Therefore, it would be better to say that sensations are replaced with intuitions, to wit, «objective representations that are akin to perceptions» in such a manner that «we do not have a sensation of an infinite Euclidean magnitude (!), but we do have a singular and immediate representation of it»[7]. To put it roughly, one has now an intimate connection between cognition as intuition and drawing, which in Kant’s parlance is also called “construction”[8]. The type of representation ascribed to space presupposes the capacity of directly exhibiting something in a sphere which is neither that which concepts enter as abstractions from experience, nor it is experience as such. The core of this position is epitomised in The Docrine of Method of Kant’s first critique, whereby the philosopher maintains that mathematics represents universals in concreto:
Philosophy confines itself solely to general concepts, mathematics cannot do anything with the mere concepts but hurries immediately to intuition, in which it considers the concept in concreto, although not empirically, but rather solely as one which it has exhibited a priori, i.e., constructed, and in which that which follows from the general conditions of the construction must also hold generally of the object of the constructed concept. Give a philosopher the concept of a triangle, and let him try to find out in his way how the sum of its angles might be related to a right angle. He has nothing but the concept of a figure enclosed by three lines, and in it the concept of equally many angles. Now he may reflect on this concept as long as he wants, yet he will never produce anything new. […] But now let the geometer take up this question. He begins at once to construct a triangle. Since he knows that two right angles together are exactly equal to all of the adjacent angles that can be drawn at one point on a straight line, he extends one side of his triangle, and obtains two adjacent angles that together are equal to two right ones. Now he divides the external one of these angles by drawing a line parallel to the opposite side of the triangle, and sees that here there arises an external adjacent angle which is equal to an internal one, etc. In such a way, through a chain of inferences that is always guided by intuition, he arrives at a fully illuminating and at the same time general solution of the question[9].
Friedman has shown that this is but the proof that the sum of the angles of a triangle equals two right angles. Furthermore, he rightly acknowledged that in this case «geometrical proofs are themselves spatial objects», as well as the character of logical demonstration is also temporal, and thus gains a physical nuance. Therefore, he says, «it is the spatio-temporal character of construction in pure intuition that enables Kant to give a philosophical foundation for both Euclidean geometry and Newtonian dynamics»[10]. At the same time, Friedman has underlined that pure intuition concerns the possibility of objects, and thus it deals with pure logical schemata to which things may adhere or not. Therefore, one should argue that the doctrine of intuition as such does not compel oneself to endorse the statement that the spatial form of the external world is Euclidean, but only that there are «rigorous methods of proof» that exploit diagrams and coincide as far as possible with the sort of proofs given in Euclid’s books[11]. If this be true, the emergence of non-Euclidean geometries would not discard the doctrine of pure intuition as such. Even Coffa noticed that «Kant had never doubted the logical consistency of non-Euclidean geometries. He would surely have said of hyperbolic geometry that it is impossible but not logically impossible (since its “negation”, Euclidean geometry, is not logically necessary but only intuitionally necessary)»[12].
Accordingly, and this is my point, when Kant rephrased his original argument to comply with his “Copernican revolution”, a shadow was cast on the former inspiration. We have seen that the mental faculties of living beings depend on the qualities of matter and that this entails, for beings that live within a given range in our galaxy, that they can form a representation of the world only through sensibility. That is to say that they cannot construct intellectual intuitions of space. Hence, theoretically at least, it would be possible either that other imperfect beings will have different shapes of intuition – a claim utterly compatible with empiricism – or that higher beings will not need sensibility to represent space. But then Kant brought intuition into play and variously argued in favour of the apodicticity of Euclidean geometry. In a nutshell, while in principle more representations of space should be possible, in practice, that is, when it comes to the construction of reality performed via the synthesis of the understanding that applies to intuitions, this is not the case[13]. Kant in fact explains that the principle of the synthesis naturally implies that between two points there is only a straight line, that two straight lines do not include any space[14], and more in general he writes the following in the second edition of his opus magnum:
Geometry is a science that determine the properties of space synthetically and yet a priori. What then must the representation of space be for such a cognition of it to be possible? It must originally be intuition […]. But this intuition must be encountered in us a priori, i.e., prior to all perception of an object, thus it must be pure, not empirical intuition. For geometrical propositions are all apodictic, i.e., combined with consciousness of their necessity, e.g., space has only three dimensions; but such propositions cannot be empirical or judgements of experience, nor inferred from them. Now how can an outer intuition inhabit the mind that precedes the objects themselves, and in which the concept of the latter can be determined a priori? Obviously not otherwise than insofar as it has its seat merely in the subject, as its formal constitution for being affected by objects and thereby acquiring immediate representation, i.e., intuition of them, thus only as the form of outer sense in general. Thus our explanation alone makes the possibility of geometry as a synthetic a priori cognition comprehensible[15].
This passage shows that the advocacy of the apriority of space is ineluctably intertwined with the assumption that there is a mind for which apriority is given. More precisely, the latter is meaningful only if the subject is meant to offer the means through which the phenomena of the external world are immediately, to wit, a priori transformed into the phenomena «of outer sense in general». It is precisely in this way that an argument allegedly sympathetic with empiricism has been transformed into the very pinnacle of Kant’s transcendental doctrine. Nevertheless, the old version resurfaces in the General Remarks on the Transcendental Aesthetic, where Kant adds:
It is also not necessary for us to limit the kind of intuition in space and time to the sensibility of human beings; it may well be that all finite thinking beings must necessarily agree with human beings in this regard (though we cannot decide this), yet even given such universal validity this kind of intuition would not cease to be sensibility, for the very reason that it is derived (intuitus derivativus), not original (intuitus originarius), thus not intellectual intuition, which for the ground already adduced seems to pertain only to the original being, never to one that is dependent as regards both its existence and its intuition (which determines its existence in relation to given objects); although the last remark must be counted only as an illustration of our aesthetic theory and not as a ground of its proof [16].
The argumentation presumably develops in this manner. (i) Intuition is coined upon the finite nature of human subjectivity. (ii) Since human understanding is derivative and not original as it would be in the case of God, external reality will appear to affect the subject in the form of intuition. (iii) That is to say that reality is something apparent for a subject who is a being made this way; (iv) so, if her constitution changed, the same would happen as to the form of the external world she senses. One may only conjecture that finite beings can reach an agreement on space as a three-dimensional and Euclidean structure[17]; however, it may be also the case that space has another shape for different living beings. In this respect, I propose to conceive of the subjectivity implied by Kant as infra-subjectivity, that is, as a ‘localist’ constitutive condition that relates to modern “correlationism” [18], realising a sort of compromise between his early and his later position. In a nutshell, while it is standardly accepted that, within a relational frame, objects and objectual complexes are given for and to subjects, I purport to have shown that Kant defended a ‘microscopic’ version of this thesis, according to which objectivities are given for and to subjects specifically endowed with a certain mind and not another[19]. In this way the plurality of minds still underpins the infra-subjectivity hypothesis.
- Von Helmholtz
In this section, I will scrutinise von Helmholtz’s approach to the philosophy of geometry. In particular, I will draw attention to the fact that to confute the notion of synthetic a priori, he notwithstanding leverages reasonings on the constitution of subjects.
In the second half of 19th century, it seems that while German philosophers were willing to turn back to Kant, scientists were wary of transcendental philosophy. In this respect, von Helmholtz makes no exception. Indeed, he mentions Kant’s erroneous view in the opening of his seminal lecture from 1870, Über den Ursprung und die Bedeutung der geometrischen Axiome, although his attack is firstly stated in a footnote. He refuses to elaborate on the position advocated by Wilhelm Tobias, and argues that it does matter whether intuition is just the point of departure for developing axioms a priori or whether the axioms are given originally with intuition itself[20].
So far, so good. But ironically, von Helmholtz starts exemplifying his view with respect to the subjective constitution of the mind. In fact, he explains that bidimensional beings do not represent space in three dimensions. Also, if one imagined them living on curved spaces, one would conclude that they cannot establish axioms on straight lines as the shortest distances between two points[21].
Figure 2––On the left, a flat space where the shortest distance between any two points is a straight line. On the right, two geodetics that represent the distance between the same two points do not measure the same, that is, the shortest distance.
Von Helmholtz openly asserts that:
It is clear that the beings that live on the sphere having the same logical capacities of the beings that live on the flat space and of us ourselves in our three-dimensional space, they must however erect a completely different system of geometrical axioms. These examples show us already that, depending on the kind of space inhabited, different geometrical axioms must be erected by beings whose intellectual forces can wholly correspond to ours[22].
In this case, it is apparent that the argument does not suffice to confute Kant because it simply asserts that beings whose intellectual faculties are comparable to ours and inhabit a world different from ours can construe different intuitions of space. As we have seen in the second section, this is precisely the possibility that Kant himself left open. It is thus possible that pure intuition is not unique, although it still exists in the sense of a weak preconditional representation: «This would suffice to display how, in this way, the series of sensitive impressions that would give a spherical or pseudospherical world - if it exists - can be derived from the well-known laws of our sensitive perceptions»[23].
However, there is a flatly anti-Kantian claim in von Helmholtz. It concerns the introduction of the concept of ‘rigid’ body, a notion that von Helmholtz believed crucial to account for measurements. It belongs to a set of five axioms that Torretti has indicated as the conceptual scaffolding of von Helmholtz’s foundation of geometry. It consists of the assumption that there are pairs of movable point-systems in space that «can be made to coincide, simultaneously or successively, with the same pair of points in space», provided that space is a n-fold extended manifold. It thus turns out that the equation that relates point-pairs «is independent of the movement of the system and is the same for all congruent pair-points»[24]. Torretti has finally summed up the novelty with respect to Kant as follows: «The role of the concept of a rigid body in the constitution of scientific experience does not consist in presiding, like a Kantian category, a purely mental process of organisation of sense-data; but in regulating the manufacture and use of material instruments of measurements»[25].
Nevertheless, two aspects may strike the reader. First, the rigid body argument is expounded after the assumption that humans cannot represent to themselves a fourth dimension in view of their perceptual structure. Second, this claim seems to have a bearing on the comparison of magnitudes. In this respect, it is worth mentioning the mental experiment that von Helmholtz used to explain his approach. Suppose one is in front of a convex mirror. In a bidimensional simplification, one would be confronted with the situation below:
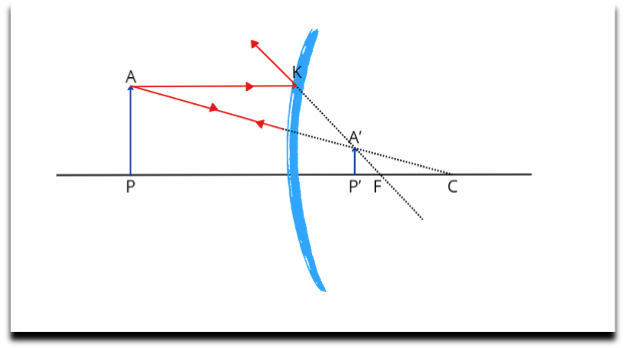
Figure 3––von Helmholtz’s convex mirror. P and P’ are conjugate points, that is, P’ maps P onto the mirror––just as A’ maps A. F is the focal point, while C represents the curvature centre. AP is a ‘real’ object and A’P’ is its virtual image onto the mirror.
This argument is provided by von Helmholtz in order to embed Beltrami’s proof that the postulate of free mobility can be satisfied not only within Euclidean geometry, but also in spaces of constant non-zero curvature[26]. In short, the Euclidean world outside the mirror will be projected onto the mirror surface and distances will be shrunken in the triangle KFP’, so while AP is mapped into A’P’, the sun and the horizon will be gathered around F. Therefore, the more one distances oneself from the mirror, the more the “flattening” of the world on the mirror becomes relevant. Roughly speaking, the mirror world contracts critically if one walks away from it, but one can still settle a one-to-one correspondence between each real-world line and plane and each line and a plane on the mirror. As a consequence, one cannot deliberate on the difference of such spaces, given that the very same number of unities of lengths are counted both in the image and the real world. Von Helmholtz writes:
The image of a man measuring with a rule a straight line from the mirror would contract more and more the farther he went, but with his shrunken rule the man in the image would count out exactly the same number of centimetres as the real man. And, in general, all geometrical measurements of lines or angles made with regularly varying images of real instruments would yield exactly the same results as in the outer world, all congruent bodies would coincide on being applied to one another in the mirror as in the outer world, all lines of sight in the outer world would be represented by straight lines of sight in the mirror. In short, I do not see how men in the mirror are to discover that their bodies are not rigid solids and their experiences good examples of the correctness of Euclid’s axioms[27].
It is striking that von Helmholtz declares that in this situation there is no possibility that one of the inhabitants of the two worlds is in a position to state which of the two is the ‘real’ one[28], provided that they can communicate with each other. Besides, for reasons of symmetry, the mirror inhabitant would see our world as a «a picture in a spherical mirror, and would speak of us just as we speak of them»[29]. How is it possible not to see here a hint of what we called infra-subjectivity?
In effect, von Helmholtz insists in the first pages of his paper on the fact that the faculty of “sich vorstellen” means but «the power of imagining the whole series of sensible impressions that would be had in such a case»[30]. Therefore, on the one hand, one may figure out how in different conditions subjects may shape their spatial cognitions; on the other hand, one may conjecture that a subject may become acquainted with a kind of ‘construction’, which will be so to speak carried by the subject with herself. Thus, by way of example, if the inhabitant of the Euclidean world with her perceptual structure moved to the mirror, she would sense that the space nearby would be unaltered given that, for small regions, it would not be possible for an observer grown up in a Euclidean world to ascertain whether she finds in a new type of space or not. But since this example seems to vulgarise the algebraic ‘fact’ that for infinitesimal regions the line element[31] can provide Euclidean metrics also in spherical or pseudo-spherical spaces, the question is whether one can be content with an analytic treatment of non-Euclidean geometries or if one still needs examples to intuit the meaning of formulae.
Von Helmholtz seeks a sort of compromise (consciously or not) and decides to defend an empiricist position, according to which the choice of metrics depends on empirical conditions of measurability. As Torretti puts it: «A mathematical theory of space which does not make allowance for the possibility of measurement does not deserve the name of geometry, since no metrein, no measuring, can be performed within its framework»[32].
Von Helmholtz’s reasoning is explained in its entirety in this excerpt:
The axioms of geometry certainly do not speak of spatial relationships alone, but also, at the same time, of the mechanical behaviour of our most rigid bodies during motions. One could admittedly also take the concept of fixed geometrical spatial structure to be a transcendental concept, which is formed independent of actual experiences and to which these need not necessarily correspond, as in fact our natural bodies are already not even in wholly pure and undistorted correspondence to those concepts which we have abstracted from them by way of induction. By adopting such a concept of rigidity, conceived only as an ideal, a strict Kantian certainly could then regard the axioms of geometry as propositions given a priori through transcendental intuition, ones which could be neither confirmed nor refuted by any experience, because one would have to decide according to them alone whether any particular natural bodies were to be regarded as rigid bodies. But we would then have to maintain that according to this conception, the axioms of geometry would certainly not be synthetic propositions in Kant’s sense. For they would then only assert something which followed analytically from the concept of the fixed geometrical structures necessary for measurements, since only structures satisfying those axioms could be acknowledged to be fixed ones[33].
Now that the postulate of rigidity is recognised as an a priori condition that lays the foundations of the concept of rigid bodies in the field of mechanics, a Kantian would be left with the discovery that the axioms of geometry cannot be synthetic a priori. Indeed, “Intuition” is nothing but
Empirical knowledge acquired in our memory through the accumulation and reinforcement of similar and recurrent impressions, and in no way a transcendental form of intuition given before all experience. I do not need here to further discuss that to such worked-through intuitions of a typical lawful behaviour, which obtained empirically and did not still amount to the clarity of the concept uttered with precision, often enough imposed to metaphysicians as propositions given a priori[34].
Scholars have intensively discussed of such an endorsement of empiricism as the result of von Helmholtz’s criticism of Kant. However, they also focus on a short addendum to Die Tatsachen in der Wahrnehumung, entitled Der Raum kann transcendental sein, ohne dass es die Axiome sind. With respect to the latter, it seems to me that von Helmholtz’s strategy is to contravene twice Kant’s claim according to which «neither space nor any geometrical determination of it a priori is a transcendental representation, but only the cognition that these representations are not of empirical origin at all and the possibility that they can nevertheless be related a priori to objects of experience can be called transcendental»[35]. First, if space can be rendered transcendental, there should be no restriction as to the choice of axioms and thus, as we have seen, no unique form of intuition. Second, all of this does not only compel us to conceive of axioms as “definitions”, but more importantly to gain them empirically. In a few words, von Helmholtz is discovering, perhaps accidentally, a new concept of the analytic which does not square with Kant’s ‘unfruitful’ decompositions of given concepts into their constituents[36]. Rather, such a refined notion refers to the impossibility of thinking of science without necessary principles[37], but it warrants that the latter are unavoidably bound with experience.
It is however hard to say whether von Helmholtz’s position can be coupled with conventionalism[38]: DiSalle argues that von Helmholtz thought having made of axioms synthetic a posteriori propositions[39]. That being said, it is von Helmholtz himself the one who notices that «in the end, only facts and neither preconceived opinions nor Kant’s authority can decide. If axioms are natural laws, it is moreover true that they obviously partake in the only approximative demonstrability of all natural laws through induction»[40]. Also, we have seen that von Helmholtz already realised that there was a circle in proving definitions via the features of bodies that should conform to such definitions[41]. Therefore, it is possible that DiSalle is right when suggesting that the only way that remained open was to consider the content of geometrical propositions as “general expectations” about the compliance of physical with ideal bodies[42]. As paradoxical as it may sound, geometry is «a formal science developed from empirical principles»[43].
Nevertheless, we also noticed that the concept of synthetic resurfaces every time von Helmholtz emphasises that a subject constructs her perceptual world according to the causality principle that puts order in her sensations. By doing so, she can also accommodate her perceptions when transposed into a new ‘geometrical’ world. The latter is consequently built in Kant’s sense since space is given for and to a specific kind of subject. One is thus vis-à-vis once again with the question concerning the meaning of examples: does they merely serve to make complex arguments available for common sense? Once that “Anschaungsnotwendigkeit” has been discarded[44], does intuition amount to an auxiliary means that provides examples? Or is one supposed to reconstruct intuition from examples? It seems to me that von Helmholtz’s approach aligns with the third option and that he does not estimate that to be Kantian. I purported to uphold that this is true only if one disentangles intuition from infra-subjectivity.
- Poincaré
In the third chapter of La science et l’hypothèse, Poincaré takes his well-known stand against Kant. To sum up, he rejects the idea that axioms are synthetical a priori propositions for in this case they would impose on our mind necessarily, that is, apodictically in Kant’s sense. He explains that:
The geometrical axioms are therefore neither synthetic a priori intuitions nor experimental facts. They are conventions. Our choice among all possible conventions is guided by experimental facts; but it remains free, and is only limited by the necessity of avoiding every contradiction, and thus it is that postulates may remain rigorously true even when the experimental laws which have determined their adoption are only approximate. In other word, the axioms of geometry (I do not speak of those of arithmetic) are only definitions in disguise[45].
In essence, when applied to physics, mathematical definitions contain implicit axioms which do not stand for self-evident truths and rule the application of mathematical ‘free creations’ to physics: «The possibility of the motion of an invariable figure is not a self-evident truth. At least it is only so in the manner of Euclid’s postulate, and not as an analytical a priori judgement would be»[46]. So, in the expression “definitions in disguise” the word definition explains that axioms are not synthetic a priori, while “in disguise” prevents us from considering them as analytic statements.
Now, this position is not utterly consistent with von Helmholtz’s since it takes a further step. Indeed, it defends the difference between geometry and physics. In this case, experience is only a guide that helps our choice, while in the theoretical field mathematical structures develop autonomously. As DiSalle put it: «That certain bodies remain congruent to themselves under certain motions is not an empirical fact about those bodies, but a definition of congruence»[47]. For this very reason, the axioms of geometry are mixed definitions implying coordination and comparison between analytic principles for which one in ‘formal’ mathematics simply need to avoid contradiction, and measurements[48].
This position is variously justified by Poincaré, but it is mostly the consequence of the existence of non-Euclidean geometries. Poincaré’s point is that these systems are possible regardless of their empirical counterparts, although they need experience for becoming effective physically. Therefore, on the one hand, geometries can be compared per se with reference to their mere structural content. This pushes Poincaré to famously uphold that Euclidean geometry is more “convenient” than non-Euclidean geometries just as a polynomial of the first degree is simpler of a polynomial of the second degree. But on the other hand, this is not the only criterion that the French mathematician mentions in defence of the “convenience” of Euclidean geometry: the latter aligns with «the properties of natural solids, those bodies that we near with our limbs and eye, and with which we forge our measurement tools»[49].
It is thus not by chance that the preference for Euclidean geometry is withdrawn when pondering over the existence of flat beings whose mind would be comparable to ours. In speaking of “implicit axioms”, and by referring to the postulate of free mobility and the assumption of congruence without making the name of von Helmholtz explicitly, Poincaré notices that:
Figures are equal when they can be superposed. To superpose them, one of them must be displaced until it coincides with the other. But how must it be displaced? If we asked that question, no doubt we should be told that it ought to be done without deforming it, and as an invariable solid is displaced. As a matter of fact, this definition defines nothing. It has no meaning to a being living in a world in which there are only fluids. If it seems clear to us, it is because we are accustomed to the properties of natural solids which do not much differ from those of the ideal solids, all of whose dimensions are invariable[50].
This proposition implies that if one had a body and a mind like ours, and lived in a world like ours, one would justify free mobility and congruence in light of Euclidean geometry; but as soon as different conditions come out, the representation of physical reality is modified accordingly.
At this point, as it happened with von Helmholtz, one is tempted to highlight that these are merely examples, which is partially true. However, in Kant’s original argument on intuition, the senses were the inescapable means that communicated to subjects the effects of the physical world. This kind of narrative is unaltered not only in von Helmholtz, but also in Poincaré. In this respect, the role of infra-subjectivity is clear: it surfaces when the use of conventions should be specified according to experience. Speaking of spherical geometries, Poincaré writes:
Let us imagine to ourselves a world only peopled with being of no thickness, and suppose these “infinitely flat” animals are all in one and the same plane, from which they cannot emerge. Let us further admit that this world is sufficiently distant from other worlds […] and while we are making these hypotheses it will not cost us much to endow these beings with reasoning power, and to believe them capable of making a geometry. In that case they will certainly attribute to space only two dimensions. But now suppose that these imaginary animals, while remaining without thickness, have the form of a spherical, and not of a plane figure, and are all on the same sphere, from which they cannot escape. What kind of geometry will they construct? In the first place, it is clear that they will attribute to space only two dimensions. The straight line to them will be the shortest distance from one point on the sphere to another––that is to say, an arc of a great circle. In a word, their geometry will be spherical geometry. What they will call space will be the sphere on which they are confined, and on which take place all the phenomena with which they are acquainted. The space will therefore be unbounded, since on a sphere one may always walk forward without ever being brought to a stop, and yet it will be finite; the end will never be found, but the complete tour can be made[51].
The clarity of Poincaré’s prose make figures unnecessary. I thus limit myself to draw the attention of the reader to these steps:
1) Geometry is constructed;
2) This construction depends on the body and the mind of the beings that inhabit the space to be described;
3) The construction also depends on the physical features of the world;
4) The intuitive shapes of figures will vary accordingly;
5) The definitions are in some sense more general than the contents of figures (e.g. the shortest distance between two points might be either a straight line or a geodesic, it is up to experience to decide which of the two constructions is the ‘convenient’ one).
(1) and (2) are compatible with Kant’s standpoint, while (3) and (4) are admitted within Kant’s early stand and are at least compatible with Kant’s later position, while (5) is more liberal with respect to Kantianism. (1), (2), (3), (4) and (5) altogether endorse a program that distinguishes at least two levels of generality that correspond respectively to conventions and their instantiations. In a manner of speaking, experience accompanies mathematics: the experience with solid bodies leads us to metrical geometry, just as the acquaintance with the rectilinear propagation of light drives us to projective geometry. But in no way it will be possible to consider geometry as an experimental science. As Einstein underlined with reference to Poincaré, it is only the sum of “axiomatic geometry” (G) and “practical geometry” (P) that can be put to test[52].
Now, that all of this is reminiscent of Kant’s approach is shown by these two excerpts:
- i) Beings whose minds were made as ours, and with sense like ours, but without any preliminary education, might receive from a suitably-chosen external world impressions which would lead them to construct a geometry other than that of Euclid, and to localise the phenomena of this external world in a non-Euclidean space, or even in space of four dimensions. As for us, whose education has been made by our actual world, if we were suddenly transported into this new world, we should have no difficulty in referring phenomena to our Euclidean space. Perhaps somebody may appear on the scene some day who will devote his life to it, and be able to represent to himself the fourth dimension[53].
- ii) If geometrical space were a framework imposed on each of our representations considered individually, it would be impossible to represent to ourselves an image without this framework, and we should be quite unable to change our geometry. But this is not the case: geometry is only the summary of the laws by which these images succeed each other. There is nothing, therefore, to prevent us from imagining a series of representations, similar in every way to our ordinary representations, but succeeding one another according to laws which differ from those to which we are accustomed[54].
Both these passages recall some of von Helmholtz’s ideas. Nevertheless, by also encompassing the possibility of representing the fourth dimension, (i) integrally accepts that minds are affected by the external space whose shape consequently depends on the adaptation to the environment. However, (ii) shows that this presupposes physics. Different representational types are introduced by Poincaré constantly in view of new physical conditions[55]. For instance, beings living on a sphere warmed at the centre, provided that the coefficients of dilatation for all bodies are the same and that a body is instantaneously in equilibrium with the environment, will experience that an object in motion will become smaller and smaller while approaching the circumference of the sphere. Therefore, «if to us geometry is only the study of the laws according to which invariable solids move, to these imaginary beings it will be the study of the laws of motion of solids deformed by the differences of temperature alluded to»[56].
That being said, one should notice that Poincaré paved the way for an integrally new way to get close to the meaning of mathematical knowledge. With respect to Cassirer, Biagioli has written that «the synthetic character of mathematics» can be rephrased «in terms of a conceptual synthesis able to generate univocally determined objects»[57]. She herself nevertheless recognised that Poincaré was a source of inspiration in such a logical reform of the concept of synthetic. Poincaré’s discussion of the notion of group is exemplary in this respect:
The object of geometry is the study of a particular “group”; but the general concept of group pre-exists in our minds, at least potentially. It is imposed on us not as a form of our sensitiveness, but as a form of our understanding; only, from among all possible groups, we must choose one that will be the standard, so to speak, to which we shall refer natural phenomena[58].
Hence, although «Poincaré’s argument referred not so much to logically equivalent geometries, as to geometries that could be considered equivalent representations of physical reality»[59], it is clear that the very content of geometrical axioms is not related to sensibility anymore. Such a content follows from the understanding which gives definitions in disguise as they should be applied to experience while remaining analytic per se - analytic in the sense that they are purely conceptual. In this way, one can cast a shadow on the synthetic a priori and even on the analytic-synthetic distinction, and strive to discard Kant’s transcendental approach[60]. However, it is Biagioli herself that reminds us once more that «assuming inhabitants of our world would find themselves in the non-Euclidean world, Poincaré believed that they would base their measurements on Euclidean geometry, rather than change their habits»[61].
- Concluding Remarks: Back to Kant?
At closer inspection, we were left with our problem: Is now intuition only an auxiliary means that is of service for providing examples? If so, would it be Kant’s doctrine a worthless incrustation that we inherited from an old-fashioned philosophy of geometry? In addition, the problem can be generalised, so much so that one should ask the following: What does it mean to give examples? Are they per se sufficient to abstract general definitions? At first glance, this does not seem to be possible[62].
However, the examples we encountered are characterised so to speak by the same plot. They hint at the implicit principle that when shifting from mathematics to physics, one is compelled to consider the sensitive structure of subjects in response to the stimuli coming from the environment. In a more sophisticated version, the sensitive structure is replaced by concepts imposed freely by the understanding upon experience.
To sum up, I have tried to show that Kant’s lesson was neither that space is Euclidean nor that it is shaped by our minds, but rather that space is made to or for our minds, which are in turn accustomed to be affected by physical reality in a certain fashion and thus to construct space accordingly. I called this argument infra-subjectivity and I proposed to relativise the standard interpretation of Kant’s intuition––if any. By borrowing Hanna’s definition, one may also dare to say that it is right that «all the proper objects of human cognition are nothing but the intersubjectively shareable contents of sensory or experiential representations»[63], but one should add that such a shareability is intrinsic only for all the minds that have a given structure in common. I thus emphasised that infra-subjectivity is correlated with the assumption that there exist other minds and even extra-terrestrial life.
Furthermore, I have not defended the idea that von Helmholtz and Poincaré were Kantian, although there are, especially concerning von Helmholtz, valuable interpretations that point in this direction[64]. I contented myself with showing that there was a touch of irony in their rejection of Kant’s arguments. Indeed, if one considers that those examples could be seen as «warm-up stories» that should «dislodge our faith in the truthfulness of intuition»[65], one is struck by the fact that their finding so much place in their works gives the opposite impression. If this can be partly explained in light of the popular writings in which these examples surfaced, it is nonetheless telling that they play such an important role for unleashing the message behind empiricism and conventionalism.
[1] Apart from Critique of Pure Reason, Kant’s works are cited according to: I. Kant, Gesammelte Schriften, Hrsg.: Bd. 1–22, Preußische Akademie der Wissenschaften, Bd. 23: Deutsche Akademie der Wissenschaften zu Berlin, ab Bd. 24 Akademie der Wissenschaften zu Göttingen, Berlin 1900ff (henceforth AA).
[2] Cf. A. Losch, Kant’s Wager. Kant’s Strong Belief in Extra-terrestrial Life, the History of This Question and its Challenge for Theology Today, in «International Journal of Astrobiology», 15, 4, 2016, pp. 261-270. Furthermore, and apart from Kant’s own assessment (see below), one cannot deny that Kant’s interest in extra-terrestrial life has a bearing on his ‘cosmopolitical’ philosophy (cf. P. Szendy, Kant chez les extraterrestres. Philosofictions cosmopolitiques, Le Minuit, Paris 2011).
[3] I. Kant, Universal Natural History and Theory of Heavens, Engl. tr. CUP, Cambridge 2012, pp. 297-298 (Ak I: pp. 354-355).
[4] Ibid., p. 301 (Ak 1: p. 359).
[5] I. Kant, Reflexionen zur Metaphysik, Ak XVII, p. 639, allegedly 1774.
[6] R. Torretti, Philosophy of Geometry from Riemann to Poincaré, Reidel, Dordrecht et al. 1984, p. 164.
[7] A. Janiak, Kant’s Views on Space and Time, in «The Stanford Enciclopedia of Philosophy» (Spring 2020), E. N. Zalta (ed.), URL: https://plato.stanford.edu/archives/spr2020/entries/kant-spacetime/ Last access: 16 December 2023.
[8] I do not agree with Coffa on this point: as I am trying to argue, one is just told of what “construction” is, viz. drawing (J.A. Coffa, The Semantic Tradition from Kant to Carnap. To the Vienna Station, CUP, Cambridge 1991, p. 44). Also, the idea that “we cannot synthesize the axioms until we have them” and that one would thus be beyond the domains of sensibility and the understanding requires further developments that are not mandatory in Kant’s own account (see Friedman’s remarks below in the text).
[9] I. Kant, Critique of Pure Reason, Engl. tr. CUP, pp. 631-632 (KrV, A715-717/B743-746).
[10] M. Friedman, Kant and the Exact Sciences, HUP, Cambridge 1992, pp. 57-58.
[11] Ibid., p. 95.
[12] J.A. Coffa, The Semantic Turn…, cit., p. 49.
[13] Reverberations of this conception must be sought in Natorp’s early defence of neo-Kantianism against metageometry and Minkowskian special relativity (P. Natorp, Die logischen Grundlagen der exakten Wissenschaften, Teubner, Leipzig und Berlin 1910). On this topic, I allow myself to recall: L. Laino, Natorp, Cassirer and the Influence of Relativity Theory on Neo-Kantian Philosophy, in Philosophers and Einstein’s Relativity, C. Russo Krauss, L. Laino (Eds.), Springer, Cham 2023, pp. 107-138.
[14] I. Kant, Critique of Pure Reason, cit., p. 288 (KrV A163/B204).
[15] Ibid., p. 176 (KrV, B40-41).
[16] Ibid., pp. 190-191, KrV, B72.
[17] Cf. M. Friedman, op. cit., p. 94.
[18] Cf. Q. Meillassoux, Après la finitude. Essai sur la nécessité de contingence, Editions du Seuil, Paris 2006.
[19] In fact, in Kant the correlationist statement has a counterpart: nature “is to be observed by reasoning beings” (A. Losch, op. cit., p. 264). This principle of situatedness bears witness to the fact that the subject is the “point of view” for which reality is given. But in order to have a point of view, there must be others (cf. P. Szendy, Kant chez les extraterrestres…, cit., p. 71).
[20] Cf. H. von Helmholtz, Über den Ursprung und die Bedeutung der geometrischen Axiome (1870), in Id., Vorträge und Reden, Vieweg, Braunschweig 18964, Bd. 2, pp. 1-33, footn. at p. 4. Indeed, in comparing Kant’s stand with von Helmholtz’s, Tobias pointed out that Kant did not mean that axioms are originally given in intuition, but only that the intuition of space may be of service for developing the axioms (W. Tobias, Grenzen der Philosophie, konstatiert gegen Riemann und Helmholtz, verteidigt gegen von Hartmann und Lasker, Müller, Berlin 1875, p. 92).
[21] This view may be at present misleading. If one indeed decomposed the curvature of a general curve in a three-dimensional space into two components, one would find out that only one of the latter is visible to inhabitants within a surface in that space. Therefore, one would have a visible “geodesic curvature” and an invisible “normal curvature”. In the case of Earth, it happens that all of the curvature is normal, so it appears that at every point of a circle the geodesic curvature vanishes (T. Needham, Visual Differential Geometry and Forms, Puman, Princeton 2021, pp. 116ff.). Nevertheless, I do not even need to underline that infra-subjectivity also weighs on this kind of explanation, because the vanishing of curvature is apparent “to the inhabitants of the surface” (ibid., p. 118).
[22] H. von Helmholtz, op. cit., p. 10.
[23] Ibid., p. 28.
[24] R. Torretti, op. cit., p. 158.
[25] Ibid., p. 168.
[26] A plenty of scholars have reconstructed the path that brought von Helmholtz out of the hypothesis that space is Euclidean. Among them, see at least: R. Torretti, op. cit., pp. 155ff.; F. Biagioli, Space, Number, and Geometry from Helmholtz to Cassirer, Springer, Cham 2016, pp. 54-65. Incidentally, Coffa has explained that von Helmholtz’s claims radicalised Beltrami’s, which aimed at tracing back hyperbolic to Euclidean geometry for two-dimensional spaces and entertained a sort of Kantian background (J.A. Coffa, op. cit., pp. 48ff.).
[27] H. von Helmholtz, op. cit., p. 25. Cited according to: R. Torretti, op. cit., p. 165.
[28] That von Helmholtz’s approach will demand a theory of relativity might be inferred from: F. Biagioli, op. cit., pp. 59-60.
[29] H. von Helmholtz, op. cit., p. 25.
[30] H. von Helmholtz, op. cit., p. 8. Cited according to: R. Torretti, op. cit., p. 165. The Kantian nuance is due to the introduction of the principle of causality as the principle of lawfulness of appearances in its relation with the temporal series of representations (cfr. B. Erdmann, Die Axiome der Geometrie. Eine philosophische Untersuchung, Voss, Leipzig 1877, p. 120; F. Biagioli, op. cit., pp. 1-21).
[31] The line element denotes the type of space in which one is in and stems from the now very well-known quadratic differential expression , whereby gμν are differentiable functions of the xn coordinates (R. Torretti, op. cit., p. 156).
[32] Ibid., p. 157.
[33] H. von Helmholtz, op. cit., p. 30, cited according to F. Biagioli, op. cit., p. 60, apart from the translation of “fest” with “rigid” when the adjective is coupled with “body”.
[34] H. von Helmholtz, op. cit., p. 31.
[35] I. Kant, Critique…, cit., p. 96 (KrV, A56/B81).
[36] For an overview on Kant’s concept of analyticity, cf. R. Hanna, Kant and the Foundations of Analytic Philosophy, OUP, Oxford et. Al. 2001, pp. 125-159.
[37] Cf. J. A. Coffa, op. cit., p. 55.
[38] Cf. R. Torretti, op. cit., p. 168.
[39] Cf. R. DiSalle, op. cit., p. 82.
[40] H. von Helmholtz, Der Raum kann transcendental sein, ohne dass es die Axiome sind, in Vorträge und Reden, cit., Bd. 2, p. 393.
[41] Cf. R. DiSalle, op. cit., p. 81.
[42] Ibid.
[43] Ibid.
[44] Cf. J.A. Coffa, op. cit., p. 53.
[45] J.-H. Poincaré, Science and Hypothesis, Engl. tr. Walter Scott, London et al. 1905, p. 50.
[46] Ibid., p. 45, modified transl.
[47] R. DiSalle, op. cit., p. 80.
[48] That Poincaré’s turn was pivotal in the history of epistemology is shown by the diffusion of the conception of “coordination” (cf. T. Ryckman, The Reign of Relativity. Philosophy in Physics 1915-1925, OUP, New York 2005).
[49] J.-H. Poincaré, op. cit., p. 50.
[50] Ibid., p. 45.
[51] Ibid., pp. 37-38.
[52] Cf. R. DiSalle, op. cit., p. 88. Cf. T. Ryckman, Einstein, Routledge, Oxon-New York 2017, pp. 264-267.
[53] J.-H. Poincaré, op. cit., p. 51.
[54] Ibid., p. 65.
[55] Friedman has explained that Poincaré needed to proceed this way for justifying his hierarchy of sciences according to which geometry cannot be derived from empirical bodies and rather is the superior layer that allows us to set forth a theory of forces on the basis of mechanical laws (M. Friedman, Reconsidering Logical Positivism, CUP, Cambridge 1999, p. 78).
[56] J.-H. Poincaré, op. cit., p. 66.
[57] F. Biagioli, Space, Number…, cit., p. 19.
[58] J.-H. Poincaré, op. cit., p. 70.
[59] F. Biagioli, op. cit., pp. 174-175.
[60] In effect, axioms just define “the indefinables”, those elements whose negation would entail contradiction. In this sense, they are “claims” and not “propositions”, which means that they are merely semantic and do not contain ‘factual’ information (J.A. Coffa, op. cit., p. 134).
[61] F. Biagioli, op. cit., p. 175.
[62] In particular, Torretti considered von Helmholtz’s Flatland example «as a didactic prop». Nevertheless, he estimated the complex mirror argument of “greater significance” (R. Torretti, op. cit., p. 392, foot. n. 27).
[63] R. Hanna, op. cit., p. 19.
[64] But especially in the sense that von Helmholtz leveraged constitutive conditions that underlie measurements, as I outlined above in the third section (cf. R. Torretti, op. cit., p. 168; F. Biagioli, op. cit., pp. 87-92).
[65] J.A. Coffa, op. cit., p. 50.
