Autore
Stefania Palumbo - Angelo Rosario Carotenuto - Massimiliano Fraldi
Università degli Studi di Trento Università degli Studi di Napoli Federico II
Stefania Palumbo PhD Student, Dipartimento di Ingegneria Civile, Ambientale e Meccanica (DICAM) – Università degli Studi di Trento Angelo Rosario Carotenuto PhD, Dipartimento di Strutture per l’Ingegneria e l’Architettura (DIST), Scuola Politecnica – Università degli Studi di Napoli Federico II
Indice
- Introduction
- Nested and hierarchical tensegrity constructs underlie the cell architecture
- The need for biological nonlinear soft-tensegrity models
- The 2-element soft-tensegrity paradigm
- The 30-element soft-tensegrity cell’s model
- Conclusions
S&F_n. 19_2018
Abstract
Tensile integrity across the scales of the living matter: a structural picture of the human cell
Tensile integrity principle governs the existence of stable constructs in which sets of pre-tensed cables and pre-compressed struts mutually interconnect according to specific topological rules and exchange forces in a way to guarantee the structure’s overall self-equilibrium. Starting from the simplest form of 2-element bow-like system, several structural components can be arranged together to assemble increasingly intricate tensegrity architectures where bars levitate sustained by a precise interplay with tensed cables, whose peculiar organization balances the vector field of axial forces. Modulation of the internal pre-stress tunes tensegrity systems towards disparate forms with different rigidities and stored elastic energies, while the floating arrangement of the compressed elements and the possible chirality confer to the whole structure pronounced deployability. This makes tensile integrity a persuasive structural paradigm for explaining and reproducing some underlying mechanisms at the basis of several dynamics experimentally observed in single cells as well as at different scales of biological architectures. In particular, by deeply exploring the intra-cellular environment, one discovers that the cytoskeleton mechanically sustains the cell’s membrane, structurally integrates cellular sub-constituents and steers migration, adhesion and division activities by behaving as a dynamic tensegrity lattice, hierarchically assembled by protein filaments, in turn made of continuously reacting polymeric tensegrity-chains at the lower nano-scale.
- Introduction
The statesman and philosopher J.C. Smuts, pioneer of the concept of holism, identified – in his book titled Holism and Evolution[1] – the single cell as well as biological organisms embodying cells populations as natural examples of holistic systems, namely systems that can’t be obtained as mere collection of their constituent parts, but rather, whose existence strictly relies on the perfect functional integration and co-operation of their components. He in fact stated:
The cell differs from the atom or molecule in its far greater complexity of structure and function, in the differentiation and specialization of its parts and organs, and in the system of co-operation among all its parts which make them function for the whole. This co-operative system exists not only in the single cell but among the multitudinous cells of organisms. The system of organic regulation and co-ordination among an indefinitely large number of parts which makes all the parts function together for certain purposes is a great advance on the system of physical equilibrium in atoms and compounds, and is yet quite distinct from the control which, at a later stage of Evolution, Mind comes to exercise in animals and humans. Mind as we know it should therefore not be ascribed to the cell or the lower organisms; but organic regulation seems on that lower level to be even more effective than Mind is at a later stage.
Within this holistic conception of the living matter as a whole greater than the sum of its parts, two (still partially open) issues arise: which type of inner structure holds up the cell by allowing the integration among its sub-constituents and the communication of each cell with the surrounding environment (i.e. neighboring cells as well as extra-cellular matrix), and how such structure participates in moulding the cellular behavior.
Actually, up to the last century, biology and medicine have ascribed a dominant, almost exclusive role in triggering and driving main cell functions ─ such as metabolism, proliferation, differentiation and motility ─ to biochemical and genetic factors. In recent years, however, several evidences have revealed that physical forces and mechanical signaling represent further pivot players in the cellular life-cycles, by contributing to the regulation of the cells activities and overall tissue development both in a causality relationship with respect to chemical and genetic signaling, and by exerting complementary actions that steer the cells functions. As a matter of fact, the experimental disclosure of the transmission of physical forces within the single-cell and across the lower scale of its sub-components and the higher one of established tissues, together with the observation of specific mechanical responses to external stimuli, corroborate the idea that cells -as well as the entire living matter when examined at different scale levels- possess a precise structural organization that obeys Mechanics conservation principles and allows the employment of the required elastic energy in cells processes. In this regard, in his commentary of 1993, the biologist and bioengineer D.E. Ingber affirmed:
the question of biological organization is the major question in biology. The molecules that make up cells and the cells that comprise tissues continually turn over; it is maintenance of pattern integrity that we call “life”. Pattern is a manifestation of structure and structural stability results from establishment of spatial relationships that bring individually destabilized structural elements into balance. Thus, a complete explanation of how cells and tissues function will come from understanding how they are put together, rather than exclusively from analysis of their substance.
A coherent interpretation of the way in which living cells could be physically organized both at the single-cell scale and at the lower molecular levels ─ at which cells components are continuously assembled and disarranged as an effect of intra-cellular reactions ─ has been proposed by the same D.E. Ingber, who individuated the aforementioned needs in what he denotes as “The Architecture of Life”: in particular, at the end of the ‘80s, Ingber suggested tensegrity structural principles as mechanical foundations of the cells intimate architecture[2].
The term tensegrity originates from the contraction of tensional integrity and was coined by the architect Richard Buckminster Fuller in the early 1950s to describe structures whose stability and integrity lie on a pervasive tensional forces state, rather than on a continuous compression as in most common (e.g. brick upon brick) constructions. Tensegrity structures are in fact constituted by disconnected pre-compressed struts integrated within a continuous network of pre-tensioned cables, their existence depending on the possibility to find specific geometrical arrangements such as forces in the pre-stressed elements can mutually balance by ensuring self-equilibrium of the whole architecture.
Actually, thanks to the peculiar spatial distribution of their elastic elements, tensegrity systems possess a number of fair characteristics which make them a persuasive structural paradigm for explaining and reproducing some underlying mechanisms at the basis of several dynamics experimentally observed in the living cells, in particular the structural stability of the in vivo cells’ scaffolds and their remodeling under the action of configurational forces driving them towards different shapes with specific mechanical properties. In fact, since their compressed constituents are disjoint, tensegrities result to be very deployable structures, capable of assuming a multiplicity of distant configurations without losing elements connections (i.e. the tensional integrity), a characteristic which can be recognized in the cells especially during migration, spreading and adhesion processes, that require extreme shape changes also triggered by the polymerization/depolymerization reactions of the cytoskeletal protein filaments. Moreover, tensegrity systems possess the intrinsic ability of storing/releasing elastic energy in the form of pre-stress relief, as well as the proper modulation of such pre-stress allows to obtain specific overall elastic properties and mechanical responses under external actions. Finally, by virtue of their predisposition to be assembled into highly organized and hierarchical constructions, tensegrity schemes can be de facto observed in living systems across the several scales: at the macro-scale (muscles-bones system), at the so called meso-scale (cells aggregates, Fig. 1A), at the micro-scale (cells, Fig. 1D-E) as well as at the nano-scale (proteins and other macromolecules, Fig. 1C-F). According to this picture, biological systems can be structurally interpreted as nested lattices of tensegrity-based architectural units, mutually and hierarchically interconnected so that the perturbation of the equilibrium of an individual unit is transmitted to the surrounding network in a way to restore and guarantee the self-equilibrium of the whole system through a feedback mechanism of forces redistribution. Such a process provides not only the structural integration and, therefore, the mechanical stability of the living matter, but it is also connected, by means of complex and partially not yet clear molecular mechanisms of mechanical-biochemical coupling, to the regulation of its physiological activities (mechanotransduction), such as proliferation or differentiation at the cell scale as well as growth, remodeling or wound healing at the tissues one.
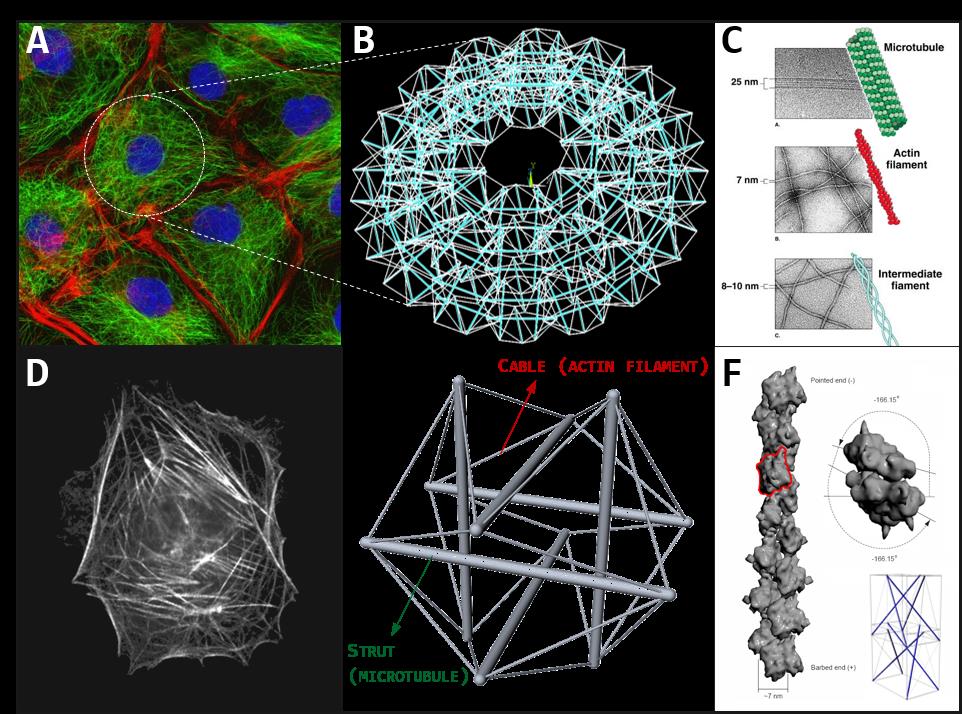
Figure 1. A. Cluster of cells imaged by fluorescence microscopy, highlighting cytoskeletal actin filaments (red) and microtubules (green). B. The cytoskeleton of the cell can be represented through tensegrities network. C. The different protein filaments of the cells cytoskeleton: microtubules, actin filaments and intermediate filaments. D. A real image of single-cell cytoskeleton. E. The structural model of the single-cell cytoskeleton: the Ingber’s 30-element tensegrity. F. The hierarchical tensegrity-based modelling of a cytoskeletal protein filament.
- Nested and hierarchical tensegrity constructs underlie the cell architecture
As recalled above, tensegrity systems live in a self-equilibrated mechanical state resulting from the interconnection between a continuous network of tension-bearing elements (cables) and floating compressed components (struts). Consequently, in absence of any external action, all their structural members already experience a state of pre-stress, whose amount dictates ─ along with the intrinsic rigidity of cables and struts — the stiffness of the whole system, otherwise unstable and collapsing at vanishing internal pre-tension.
Tensile integrity principle can be readily recognized in macro-scale bio-systems at the tissue level, such as in the bone-tendon-muscles apparatuses that regulate the vertebrates locomotion[3], as well as, with less immediacy, at the lower microscopic and sub-microscopic level: similar structural behaviors have been in fact experimentally found in eukaryotic cells. Primarily, several evidences (e.g. Traction Force Microscopy, Electron Scanning Microscopy) have shown that single-cells are characterized by an internal channeling and an inside/outside transmission of mechanical forces, which appear to be mainly generated and borne by the cytoskeletal architecture. The dense distribution of filaments that constitute the cytoskeleton de facto seems to behave like a discrete mechanical network, that confers stability and rigidity to the whole cell through a state of actomyosin-based contractile pre-stress and that reacts to the extra-cellular mechanical stimuli through a global and coordinated rearrangement of its elements, analogously to what happens in modular tensegrity units hierarchically interconnected so that the perturbation of the equilibrium of an individual component is transmitted throughout the surrounding network. Specifically, the mechanical properties of the cytoskeletal lattice arise from the complex interaction of filamentous biopolymers, namely actin microfilaments, microtubules and intermediate filaments, that continuously remodel by initiating polymerization/depolymerization dynamic processes, on the basis of the current cell needs when specific stimuli are experienced. By resembling tensegrity cables, actin microfilaments bear tensile stress, which is generated both actively, through ATP-driven processes (contractile actomyosin motors), and passively, through cell spreading and cytoplasmic pressure-induced swelling, while microtubules balance the whole network by undergoing compression, thus acting as struts-like components. On the other hand, recent studies suggest that intermediate filaments would intervene only when cells are highly strained, by operating as tensed lateral stabilizing support for nuclear form and for microtubules, thus also increasing the bending stiffness of the latter. On these bases, tensegrity principles are able to provide an effective and physically coherent description of the possible complex microstructural processes underlying the cellular behavior, by explicitly modeling both the (re)distribution of mechanical forces in the inner cytoskeletal network as the source of the cell’s stiffness and stability, and the reconfigurational mechanisms occurring, by way of example, during adhesion events, that determine a switch from round-shaped configurations to flatten adherent ones, as well as during re-orientation and migration phenomena through which cells spread by means of lamellipodia movements under external signaling.
In addition, by surveying the deep cell architecture, many works have demonstrated that tensegrity structures can be traced at different scales in the form of organized nested architectures. For instance, the same D.E. Ingber hypothesized that the cell nucleus may itself be modeled by using a separate tensegrity structure, in which single chromatin fibers (containing tightly wound coils of DNA) take the place of isolated compression-resistant elements that interconnect with a surrounding nuclear matrix under continuous tension. Such nuclear structure results to be then hierarchically linked to the surrounding cytoskeletal tensegrity (nucleated tensegrity cell model) by means of actin and intermediate microfilaments, that, acting as rods, transmit forces so as to induce coordinated (passive) nuclear shape changes when the entire cell undergoes mechanical distortions, as also observed experimentally during movement and stretching in living cells and as confirmed by the expansion of nuclear pores during cell spreading.
All these processes characterize the enormous complexity of mechanotransduction phenomena driving the main physiological activities of the cells: the activation of an intricate cascade of reactions and molecular pathways kindle a fully interlaced mechanical-biochemical coupling deputed to convert chemical gradients into entropic-elastic effects and viceversa.
- The need for biological nonlinear soft-tensegrity models
In the most of the scientific literature works, the mechanical response of tensegrities is studied under the assumption of infinitely rigid compressed struts and tensed cables reacting as linear elastic elements. Some recent papers have then included for the struts the possibility of undergoing small axial contraction before buckling occurs when the net compression induced by the adjacent cables achieves the Euler’s critical load. However, the limit of small strains – for both cables and struts – is largely exceeded when tensegrities model biological structures, especially in the case of the cell cytoskeleton for which ad hoc improvements with respect to standard models have to be taken into account.
Actually, the cytoskeletal apparatus generally experiences very large deformations as an effect of the severe stretch levels accompanying cells activities (adhesion, migration, duplication, etc.), as well as of the intrinsic compliance of its filaments. From the mechanical point of view, both actin microfilaments and microtubules are indeed soft structures, interpretable respectively as cables and struts whose difference in terms of axial rigidity amounts to less than one order of magnitude. Furthermore, it has been experimentally observed that in vivo microtubules can lie in bent/buckled configurations. All these considerations lead to the necessity of enriching standard tensegrity models for biological systems, by inevitably substituting the rigid struts with axially deformable (compressible) and bendable elements, and by providing full (i.e. both geometrical and constitutive) nonlinearity of both cables and struts, through the adoption of hyperelastic stress-strain laws.
On these bases, a completely nonlinear soft-tensegrity is conceived to more coherently model structural elements experiencing finite (rather than infinitesimal) strain regimes due to high levels of internal pre-stress and/or severe external loads. This also allows to overcome the constitutive limitations of Hooke’s elasticity at large contractions: as an example, the stress-strain law obtained from a Saint Venant-Kirchhoff bar under uni-axial tension leads to inconsistent and paradoxical finite (rather than infinite) nominal stress when the axial stretch approaches zero.
Motivated by these evidences, an archetype of nonlinear soft-tensegrity is presented in what follows: starting from an illustrative example of a simpler 2-element soft-tensegrity paradigm, the mechanical effects of nonlinear assumptions combined with buckling instability are investigated and then applied to the well-known 30-element icosahedral tensegrity structure firstly proposed by Ingber to characterize the cytomechanics.
- The 2-element soft-tensegrity paradigm
The 2-element tensegrity paradigm figures as a bow-like structure, in which a single hyperelastic tensed cable is connected at its edges to a compressed and axially deformable strut, which can severely contract in combination with possible buckling instability. By adopting a standard (incompressible) neo-Hookean hyperelastic model to trace large deformations[4], different equilibrium states can be explored by varying the internal pre-stress state to find non-trivial behaviors. In particular, the ratio between the lengths (at rest) of the elements and the ratio between their stiffness moduli mainly interplay in the tensegrity form-finding problem to determine, for different combinations, both straight and buckled configurations of the bow. These key parameters also govern the load-induced mechanical response of the system, during which additional instability phenomena (e.g. Euler’s and snap-through buckling) can be predicted. Despite of its elementary architecture, this example provides a great variety of non-trivial responses, that can be applied to well mimic the working principle of several biomechanical systems, such as robotic modules realized to reproduce the mechanics of snake locomotion or, by focusing on the cell environment, to better describe ─ with respect to literature assumptions ─ the possibility that cytoskeletal (bendable) microtubules buckle due to the compression induced by the connected tensed actin microfilaments, so demonstrating that the coupling of hyperelasticity and axial deformability of both cable and strut with bar instability can be utilized to more accurately model the experimentally observed structural mechanisms characterizing the complex intracellular scaffold.
- The 30-element soft-tensegrity cell’s model
The cytoskeletal micro-architecture of a round-shaped cell is commonly modeled by adopting a regular icosahedral 30-element tensegrity structure (shown in Fig. 1E), equipped with linear elements and rigid struts, capable to account, at least qualitatively, for a number of mechanical properties and dynamics of deformation observed in living cells. By following the strategy suggested by the 2-element paradigm, the 30-element tensegrity micro-structural model can be improved so as to include axial neo-Hookean hyperelastic elements and bendable (eventually buckling) struts, in order to take into account cell large deformations by additionally providing the possibility for microtubules to buckle in some cell districts, as experimentally observed. More in detail, the structure is made up of 6 floating pre-compressed struts, which represent cell microtubules, interconnected at the ends with a continuous network of 24 pre-tensed cables, representing the actin microfilaments. The form-finding problem of the enriched tensegrity, that provides the self-equilibrated pre-stressed (externally unloaded) structure’s configurations, can be studied and then used to characterize the cell’s mechanical response under canonical loading conditions, i.e. elongation, contraction, shear and torsion by means of standard approaches of structural engineering.
In medias res, the geometrical relationship – dictated by the regularity of the structure – between the struts’ and cables’ pre-stretched lengths ─ say L*S and L*C respectively ─ gives a compatibility equation for the corresponding pre-stretches λ*S and λ*C:
λ*S= √6/4 LC/LS λ*C
with L*S, L*C being the lengths at rest, while equilibrium equation between the struts compression force N*S and the tension in cables N*C reads
N*S = ─ √6 N*C .
By setting cell-specific geometrical and constitutive parameters, the form-finding of the tensegrity exclusively depends on the cables pre-stretch in a way that the elastic energy reservoir increases nonlinearly with it, while the overall size of the structure decreases.
This implies that cells can accumulate energy to be potentially expended for activating reconfiguration as well as migration processes, and can opportunely shrink by modulating the tension of its actin filaments, an ability exploited for example during the duplication phase or the slipping through narrow channels.
By constraining the self-equilibrated tensegrity at a rigid substrate, external perturbations are prescribed in a way to reproduce elongation/contraction, shear and torsion of the whole system, conditions naturally experienced in vivo by cells (see Fig. 2) or that can be artificially induced in order to test its mechanical response. By appealing to the standard minimal energy principle, the tensegrity model allowed to quantitatively estimate the cell’s mechanical response to the aforementioned solicitations, in terms of its axial, shear and torsional stiffness, respectively, their values being of the order of 100-1000 Pa, in full agreement with the literature experimentally measured cell stiffness. This makes cell-inspired tensegrity a powerful tool to theoretically predict some leading mechanical behaviors of single and collective cells. By way of example, endothelial cells that tesselate the tunica intima of blood vessels deform under the action of continuous flow-induced shear stresses. Moreover, the understanding of the deformation dynamics of cells structure is of key importance to examine how osteocytes -bone cells that inhabit the lacunae occurring within the interstitial spaces between osteon lamellae- work as mechano-trasducer of bone remodelling. They in fact sense the mechanical shear stresses associated with both the deformation of the solid bone structure and the interstitial fluid movement and, by acting as a mechanical filter during the remodelling process, amplify the local micro-strains to translate the mechanical stimulus into chemical signaling pathways that can recruit osteoclast and osteoblast cell types and mediate their activities in order to maintain tissue homeostasis by balancing bone tissue removal and formation. Also, fibroblasts are severely stretched when they lie in the adherent configuration, therefore their inner cytoskeletal tensegrity appears highly contracted in its height and in-plane elongated by forming a great number of focal adhesions. Interestingly, contraction and shear dynamics of the tensegrity could permit to follow the way in which the fibroblast progressively lies down from its not adherent up to the spread shape, when it starts to project several filopodia. In addition, the tensegrity approach would explain the dynamics of the single-cell during collective phenomena. For instance, the epithelial cells can exhibit collective migration dynamics with coherent angular movements, e.g. during the healing of circular wounds or during gastrulation, the latter being a morphogenetic process thanks to which epithelial cells pass from a sheet configuration to a multi-layered spheroidal one known as gastrula, from which they start to differentiate. During these movements, cells continuously experience coupled torsion-contraction conditions, and tensegrity could thus unveil the way through which cytoskeletal re-organization permits rotational rearrangement over the followed trajectories. Finally, some cell types, such as invasive tumor cells, are able to squeeze -for example- when migrating through blood vessels (e.g. arteries) that branch into capillaries having diameters smaller than the cell average dimension. Such a condition can be well described by an extreme elongation of the 30-element tensegrity cell model.
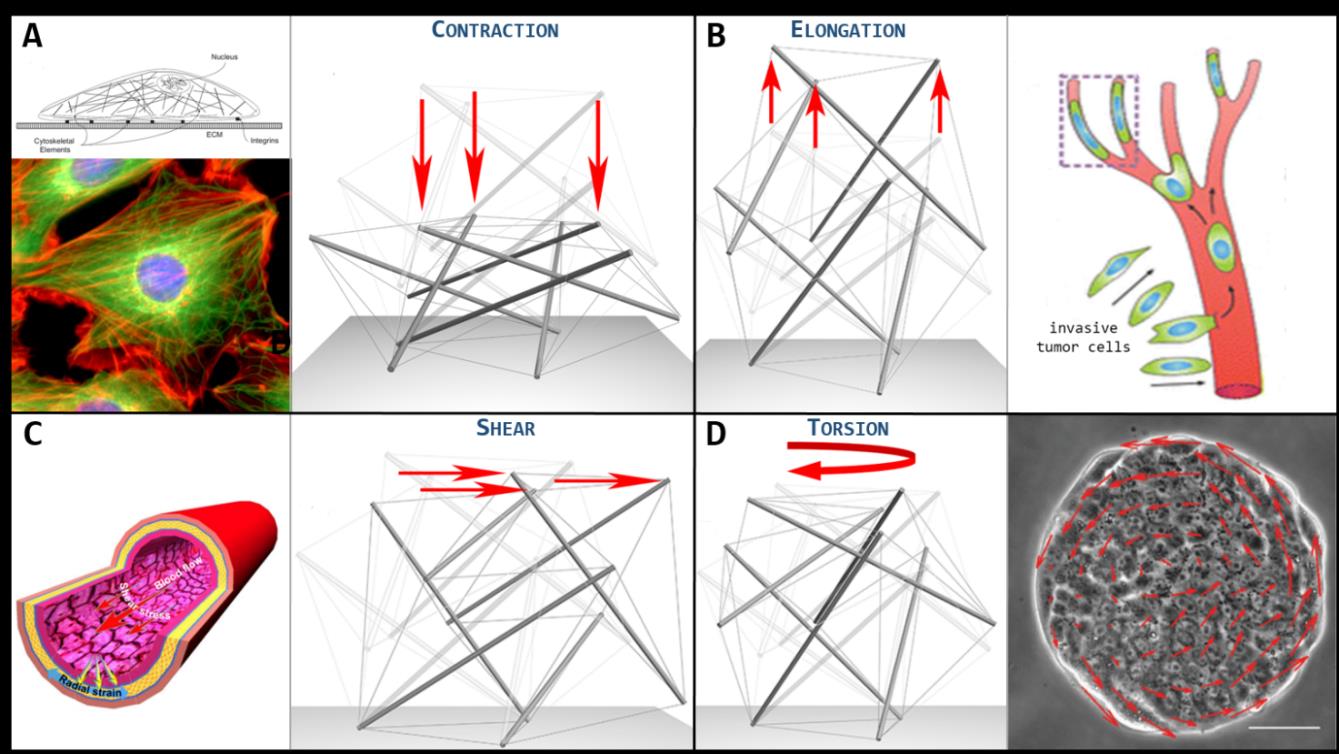
Figure 2. A. Cell stretched and flattened while adhering on a substrate. Beside, the 30-element tensegrity cell model deformed under contraction. B. Invasive tumor cells squeezing while migrating through blood vessels. Beside, the 30-element tensegrity cell model deformed under elongation. C. Endothelial cells coating the tunica intima of a blood vessel deform under the action of continuous flow-induced shear stresses. Beside, the 30-element tensegrity cell model deformed under shear. D. Collective migration of cells coupled with dynamic rotation. Beside, the 30-element tensegrity cell model deformed under torsion.
It is also worth to highlight that collective tensegrity-based dynamics let envisage the way in which cell aggregates overall respond to harmonic mechanical stimuli, by contemporarily incorporating the effects produced on the single cells. In this context, cytomechanics has a primary role in describing the ultrasound–cells interactions: positive effects have been experimentally observed on human airway smooth muscle cells, cardiac and bone cells, which showed increased proliferation, differentiation and cytoskeleton remodelling.
The prediction of mechanical responses of specific cell types is however diriment especially in the light of recent experimental evidences according to which healthy and malignant cells (of the same cell line) exhibit a significant gap in elastic stiffness, the metastatic cells being about 70% more compliant than the normal counterpart. Firstly, at least qualitatively, this difference can be actually explained in the light of the presented approach. In fact, metastatic cells generally live in configurations close to the suspended round state, which makes them more prodromal to motion, while healthy cells highly adhere to the extra-cellular environment: by reading the cell as a tensegrity system, this means that the level of cytoskeleton pre-stretch in tumor cells is considerably lower than the one attained by normal cells, this affecting the value of the global cell stiffness. This information is fundamental since a different stiffness suggests a different harmonic response, the cytoskeletal structure actually behaving like a building or a bridge, for which the calculation of resonant frequencies (basically proportional to the rigidity) that induce uncontrolled vibration of the structure up to its collapse represents a standard argument. In the case of a multi-cellular environment, say a "cell-city", the net discrimination of tumor and healthy cell mechanical responses would therefore permit, at least in principle, to selectively induce the resonance, and therefore the disruption, of sole cancer cell types by opportunely tuning the frequencies of the ultrasound stimulation on tumor-specific band. Aggregates inhabited by both tumor and healthy tensegrity-based cells with different actual stiffness could be therefore ad hoc simulated in-silico to evaluate the overall harmonic response of the system and predict the frequencies that maximize the outcomes both in terms of destructive effects on tumor cells and of healthy cells preservation. In this sense, a break-through use of engineering principles would support oncology both to design biomechanically-based devices to perform cancer detection and to prospect innovative and mini-invasive therapeutic strategies based on the use of low-intensity ultrasounds to selectively attack cancer by exploiting mechanical energy, with the further advantage to avoid some in loco complications such as the thermal ablation of the tissue.
- Conclusions
The great book, always open and which we should make an effort to read, is that of Nature.
The creation continues incessantly through the media of man. But man does not create... he discovers.
Antoni Gaudí
By fancying to travel across the dimensional scales of living matter, a man visiting the cell interior would certainly astonish as he was crossing the threshold of a majestic Cathedral, in presence of the uniqueness of the intra-cellular scenario.
Passed the marquee that envelopes and protects the cell’s microscopic world, the man would discover an extremely organized building that delimits the cellular districts by sustaining the several cell’s organelles. He would probably move uncertain steps throughout a thick forest of piled-up tubulin trees from which intricate networks of filamentous actin crowns branch, together orchestrating a fascinating and hardly decipherable structural play.
In the meanwhile, cell sub-units would ignore the visitor and continue to carry out their complementary tasks, perfectly cooperating together to the cell vital functions by unceasingly operating like they were players meticulously directed by a transcendent puppeteer of a Truman’s show-like confined universe, where everything repeats under a close dome.
The man’s admiration would be however alarmed by finding out that the structure over his head is itself living and undergoes catastrophic spatial re-configurations in order to decide the survivor of the cell. He would probably fear for his life before marveling in staring at the way in which the cytoskeletal microtubules ─ enormous pillars in his eyes ─ gradually lie down and severely contract by lowering the membrane vault height while filaments continuously disrupt and re-assemble at different points for determining the adequate tensioning that guarantees new physical equilibrium and building stability. Such movements cyclically shake the entire intracellular world during cell’s adhesion, migration and more dangerous division processes, and would sound to the man like quakes before the order is re-established.
Probably, a visionary man like Antoni Gaudí would have avidly taken inspiration in the course of his life from the magnificence of the microscopic side of Nature.
Unveiling of the cell’s inner organization and understanding the principles at the basis of the functions of the cell’s structure allows to thin out the boundaries between physics, biology and medicine and reveals how the determined properties can be exploited up to manipulate the cells’ fates. This requires a strict integration and cooperation among the different life sciences but represents, by virtue of the increasingly advancing technological media at one disposal nowadays, a realistic goal that can make engineered-based strategies move significant steps forward in the direction of a targeted, precise medicine.
[1] Smuts, J. C., Holism and evolution, by General the Right Honorable J. C. Smuts, 1926
[2] D.E. Ingber, Cellular tensegrity: defining new rules of biological design that govern the cytoskeleton, in «Journal of Cell Science», 1993.
[3] J. Gray, How animals move, Cambridge University Press 1953.
[4] D. Bigoni, Nonlinear Solid Mechanics - Bifurcation theory and material instability, Cambridge University Press 2012.








